Monoid: algebra w służbie programisty
Wiele osób zaczynających przygodę z programowaniem funkcyjnym, prędzej czy później natrafia na takie pojęcie jak monoid. Totalnym żółtodziobom w dziedzinie programowania funkcyjnego, takim jak ja, zrozumienie teorii za nim stojącej oraz poznanie sensu jego praktycznego wykorzystania zajmuje jakiś czas.
Tym postem postaram się zaoszczędzić trochę tego czasu, przybliżając w sposób minimalny, ale wystarczający do zrozumienia tego zagadnienia, opis matematyczny monoidu, a także prezentując przykładowe jego implementacje w języku Scala.
Zacznijmy od teorii
W telegraficznym skrócie, monoid1 to półgrupa2, która posiada element neutralny. Półgrupa to grupoid3, którego działanie jest łączne. Natomiast grupoid to zbiór ze zdefiniowanym działaniem. Wszystko jasne. Zacznijmy więc od początku (w tym przypadku - od końca).
Grupoid (ang. magma) to struktura algebraiczna, którą definiuje się jako zbiór \(\mathsf{M}\) z pewną operacją \(\otimes\) spełniającą następujący warunek:
\[\forall {a,b} \in \mathsf{M}: {a} \otimes {b} \in \mathsf{M}\]Krótkie przypomnienie matematyki ze szkoły średniej: znak \(\forall\) oznacza duży kwantyfikator, który czytamy jako “dla każdego”. Oprócz niego istnieje także mały kwantyfikator \(\exists\). Czyta się go jako “istnieje”.
Półgrupa (ang. semigroup) to grupoid, którego operacja \(\otimes\) jest łączna, tzn.:
\[\forall {a,b,c} \in \mathsf{M}: ({a} \otimes {b}) \otimes {c} = {a} \otimes ({b} \otimes {c})\]Czasem działanie to rozszerza się także o przemienność:
\[\forall {a,b} \in \mathsf{M}: {a} \otimes {b} = {b} \otimes {a}\]Mówimy wtedy o półgrupie przemiennej (lub bardziej formalnie: półgrupie abelowej). Dzięki tym własnościom, kolejność w jakiej wykonujemy działanie \(\otimes\) jest nieistotna. We wszystkich możliwych kombinacjach wynik będzie ten sam. Jeżeli spotkałeś się z obliczeniami rozproszonymi lub algorytmami typu MapReduce, to powinieneś zwrócić szczególną uwagę na przydatność tej własności. Dzięki niej, możemy w bardzo prosty sposób zrównoleglizować nasze obliczenia!
Posiadając półgrupę możemy w końcu zdefiniować nasz monoid. Jest to półgrupa, posiadająca element neutralny (zerowy) \(\mathsf{e}\), taki że:
\[\exists {e} \in \mathsf{M} \ \ \forall {a} \in \mathsf{M}: {a} \otimes {e} = {e} \otimes {a} = {a}\]Możemy więc zapisać monoid jako trójkę \(\{ \mathsf{M} , \otimes , {e} \}\), gdzie:
\(\mathsf{M}\): zbiór elementów,
\(\otimes\): operacja łączna (i przemienna) zdefiniowana na zbiorze \(\mathsf{M}\),
\({e}\): element neutralny.
Przykładowe monoidy
Najprostszym monoidem jest zapewne monoid, którego zbiorem jest zbiór liczb naturalnych, a operację na nim zdefiniowaną stanowi operacja dodawania. W takim przypadku elementem zerowym tego monoidu jest liczba zero.
- łączność
- \[(2 + 3) + 7 = 2 + (3 + 7) = 12\]
- element neuralny
- \[5 + 0 = 0 + 5 = 5\]
W życiu każdego programisty istnieje kolejny, bardzo często używany monoid: string.
- łączność
- \[( {ala} + {ma} ) + {kota} = {ala} + ( {ma} + {kota} ) = {ala ma kota}\]
- element neutralny
- \[{ala} + {""} = {""} + {ala} = {ala}\]
Zauważ, że w przypadku konkatenacji stringów kolejność ma znaczenie. Operacja na nich zdefiniowana jest więc łączna, ale nie przemienna.
Spróbujmy teraz znaleźć takie działanie, które w sposób naturalny nie jest monoidem. Żeby nie szukać długo rozważmy najpopularniejszą statystykę, czyli średnią ze zbioru liczb. Bardzo łatwo wykazać, że trójka składająca się ze zbioru liczb naturalnych, operacji średniej arytmetycznej \(\odot\) i zera nie jest monoidem:
\[({2} \odot {4}) \odot {6} = 4.5 \not= {2} \odot ({4} \odot {6}) = 3.5\]Istnieje jednak sposób liczenia średniej za pomocą monoidów. Zanim do tego przejdziemy, stwórzmy interfejs monoida w Scali.
Monoid w Scali
Stwórzmy trait w Scali reprezentujący monoid. Jak zdefiniowaliśmy wcześniej, każdy monoid składa się ze zbioru elementów, operacji na nim zdefiniowanej i elementu zerowego. Nasz trait będzie więc generyczny typu T i musi definiować dwie metody: zero oraz op. Dla bardziej przejrzystego API dodałem także obiekt towarzyszący.
trait Monoid[T] {
def zero: Monoid[T]
def op(a: Monoid[T], b: Monoid[T]): Monoid[T]
}
object Monoid {
def op[T](a: Monoid[T], b: Monoid[T]): Monoid[T] = a.op(a, b)
}
Spróbujmy teraz napisać klasę rozszerzającą interfejs Monoid i opakować w nią operację liczenia średniej arytmetycznej w taki sposób, żeby operacja ta była łączna (a nawet przemienna!).
case class Average[T](count: Long, sum: T)
(implicit numeric: Numeric[T]) extends Monoid[T] {
override def zero: Monoid[T] = Average(0l, numeric.zero)
override def op(a: Monoid[T], b: Monoid[T]): Monoid[T] = (a, b) match {
case (Average(countA, sumA), Average(countB, sumB)) =>
Average(countA + countB, numeric.plus(sumA, sumB))
case _ => throw new IllegalArgumentException
}
}
object Average {
def apply[T](value: T)(implicit numeric: Numeric[T]): Average[T] = Average(1l, value)
}
So far, so good. Operacje wyliczania średniej sprowadziliśmy do zliczania ilości elementów oraz sumowania wartości. Zarówno inkrementacja jak i dodawanie są monoidami, więc opierając działanie naszej struktury o inne monoidy też otrzymamy monoid!
Sprawdźmy teraz naszą klasę pod kątem łączności jej operacji:
scala> Monoid.op(Monoid.op(Average(2), Average(4)), Average(6))
res0: Monoid[Int] = Average(3,12)
scala> Monoid.op(Average(2), Monoid.op(Average(4), Average(6)))
res1: Monoid[Int] = Average(3,12)
Jak widać, wynik jest taki jaki oczekaliśmy. Koleność wykonywania działania nie ma znaczenia, ponieważ wynik jest ten sam w każdym przypadku.
Trudniejszy przykład
Podnieśmy poprzeczkę i zaimplementujmy monoid dla filtru Blooma. Filtr Blooma4 jest to struktura stworzona przez Burtona H. Blooma w 1970 r, która pozwala stworzyć skończoną reprezentację dowolnego zbioru danych.
Struktura ta składa się z \({m}\)-bitowej tablicy, oraz \(k\) funkcji haszujących o zbiorze wartości \([0;{m})\) każda. Dodanie elementu polega na obliczeniu \({k}\) wartości funkcji haszujących tego elementu i na ich podstawie ustawieniu flag w tablicy bitowej.
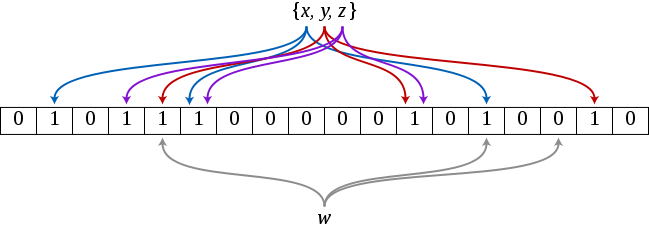
Sprawdzenie elementu również sprowadza się do policzenia tych samych haszy co przy wstawianiu elementu. Następnie sprawdzamy wartości wyznaczonych pól w tablicy. Jeżeli przynajmniej jedno pole ma wartość równą zero, to możemy być pewni, że element ten nie należy do zbioru. Inaczej sytuacja ma się wtedy, kiedy wszystkie wyznaczone pola są jedynkami. Mówimy wtedy, że element ten należy do zbioru z pewnym prawdopodobieństwem. Prawdopodobieństwo pomyłki (ang. false positive) zależy od rozmiaru tablicy bitowej oraz ilości (i jakości) funkcji mieszających. Wynosi ono:
\[{error} = (1 - {e}^{-kn/m})^{k}\]gdzie \({n}\) to ilość elementów, które wstawiliśmy do zbioru. W przejrzysty sposób działanie algorytmu przedstawił na swojej stronie Jason Davies.
Zanim zaimplementujemy nasz filtr Blooma, stwórzmy klasę funkcji haszujących. W tym celu posłużyłem się dość powszechnym algorytmem FNV5 (od pierwszych liter nazwisk autorów: Fowler-Noll-Vo), a dokładnie wariantem FNV-1a.
class HashFunction(private val base: Int) {
private val OffsetBasis = BigInt("14695981039346656037")
private val Prime = BigInt("1099511628211")
def apply(data: Array[Byte]): BigInt = data.foldLeft(base * OffsetBasis) {
case (hash, byte) => (hash ^ (byte & 0xff)) * Prime
}
}
Sam algorytm jest dość prosty, bazuje głównie na mnożeniu przez liczbę pierwszą oraz operacji alternatywy wykluczającej (XOR). Operuje on jednak na pojedynczych bajtach. By rozwiązać ten problem, stwórzmy trait Hashable, który zapewni nam konwersję typu Int oraz String na tablicę bajtów w sposób domniemany.
trait Hashable[T] {
def toByteArray(elem: T): Array[Byte]
}
object Hashable {
implicit object IntHashable extends Hashable[Int] {
override def toByteArray(elem: Int): Array[Byte] = {
val buffer = ByteBuffer.allocate(4)
buffer.putInt(elem)
buffer.array()
}
}
implicit object StringHashable extends Hashable[String] {
override def toByteArray(elem: String): Array[Byte] = elem.toCharArray.map(_.toByte)
}
}
Mając już wszystkie wymagane elementy możemy przejść do definicji filtru Blooma. Jako argumenty przyjmuje on, oprócz zdefiniowanych przed chwilą obiektów Hashable, parametry \(m\) oraz \(k\).
class BloomFilter[T](val m: Int, val k: Int)
(implicit val hashable: Hashable[T]) {
private val table: Array[Boolean] = Array.fill(m){false}
private val hashFns: Seq[HashFunction] = (0 until k).map(new HashFunction(_))
def add(elem: T): Unit = keys(elem).foreach(key => table.update(key, true))
def contains(elem: T): Boolean = !keys(elem).exists(key => !table(key))
private def keys(elem: T): Seq[Int] = hashFns
.map(_(hashable.toByteArray(elem)))
.map(hash => (hash % m).toInt)
}
Inicjalizacja obiektu polega na utworzeniu \(m\)-elementowej tablicy boolowskiej, której każdy element jest domyślnie ustawiony jako false. Dodatkowo tworzone jest \(k\) funkcji mieszających. Metody add oraz contains służą odpowiednio do wstawienia elementu do tablicy oraz sprawdzenia, czy element ten już się w niej znajduje.
Sprawdźmy, jak wygląda korzystanie z naszej struktury:
scala> val bf = new BloomFilter[String](100, 4)
scala> bf.contains("word")
res0: Boolean = false
scala> bf.add("word1")
scala> bf.contains("word")
res1: Boolean = false
scala> bf.contains("word1")
res2: Boolean = true
Dla przypomnienia: jeżeli metoda contains zwraca wartość false, to możemy być pewni, że dany element nie należy do zbioru reprezentowanego przez ten filtr Blooma. Jeżeli jednak zwrócona wartość to true, nie mamy wtedy pewności. Możemy powiedzieć, że element ten należy do zbioru, ale teza ta obarczona będzie błędem, którego wartość oszacowaliśmy wyżej.
Ostatnim etapem naszej przygody będzie stworzenie monoidu, który posłuży jako opakowanie dla naszego filtru. Jak już wiemy, każdy monoid składa się z działania oraz elementu zerowego. Możemy zdefiniować je jako:
- działanie
- \[\forall {a,b} \in \mathsf{F}, \\ {a} = \{ {a}_{0}, \dots, {a}_{m}, {h_1}, \dots, {h_k} \}, \\ {b} = \{ {b}_{0}, \dots, {b}_{m}, {h_1}, \dots, {h_k} \}: \\ {a} \otimes {b} = \{ {a}_{0} \vee {b}_{0}, \dots, {a}_{m} \vee {b}_{m}, {h_1}, \dots, {h_k} \}\]
- element zerowy
- \[{e} = \{ {false}, \dots, {false}, {h_1}, \dots, {h_k} \}\]
Nasz filtr przedstawmy jako case klasę składającą się z tablicy bitowej i funkcji haszujących. Te dwa elementy jednoznacznie charakteryzują naszą strukturę.
case class BloomFilter[T : Hashable](table: Array[Boolean], hashFns: Seq[HashFunction])
extends Monoid[T] {
override def zero: Monoid[T] = BloomFilter.zero[T](table.length, hashFns.size)
override def op(a: Monoid[T], b: Monoid[T]): Monoid[T] = (a, b) match {
case (BloomFilter(tableA, hashFnsA), BloomFilter(tableB, hashFnsB))
if tableA.length == tableB.length && hashFnsA.size == hashFnsB.size =>
BloomFilter(mergeTables(tableA, tableB), hashFnsA)
case _ => throw new IllegalArgumentException
}
// Suma logiczna elementów dwóch tablic m-bitowych
private def mergeTables(tA: Array[Boolean], tB: Array[Boolean]): Array[Boolean] =
tA.zip(tB).map {
case ((a, b)) => a || b
}
}
Cała magia kryje się w metodzie op, która wykonuje sumę logiczną tablic dwóch przekazanych jej filtrów i zwraca ją jako nową instancję filtru Blooma.
object BloomFilter {
def apply[T : Hashable](m: Int, k: Int)(elem: T): BloomFilter[T] = {
val table = getTable(m)
val hashFns = getHashFns(k)
val keys = getKeys(elem, hashFns, m)
keys.foreach(table.update(_, true))
BloomFilter(table, hashFns)
}
def zero[T : Hashable](m: Int, k: Int): BloomFilter[T] = {
val table = getTable(m)
val hashFns = getHashFns(k)
BloomFilter(table, hashFns)
}
def contains[T : Hashable](filter: BloomFilter[T], elem: T): Boolean = {
val keys = getKeys(elem, filter.hashFns, filter.table.length)
!keys.exists(key => !filter.table(key))
}
private def getTable(m: Int): Array[Boolean] = Array.fill(m){false}
private def getHashFns(k: Int): Seq[HashFunction] = (0 until k).map(new HashFunction(_))
private def getKeys[T : Hashable](elem: T, hashFns: Seq[HashFunction], m: Int): Seq[Int] =
hashFns
.map(_(implicitly[Hashable[T]].toByteArray(elem)))
.map(hash => (hash % m).toInt)
}
Kod obiektu towarzyszącego też nie należy do zbyt skomplikowanych. Metody apply i zero służą do tworzenia odpowiednio instancji filtru dla zadanego elementu, oraz pustej struktury. Poza tym funkcja contains pozwala sprawdzić, czy filtr zawiera dany element czy nie.
Sprawdźmy jak możemy wykorzystać nasz kod w praktyce. Najpierw stwórzmy fabrykę do mapowania ciągów znaków na filtr Blooma.
val bfBuilder = BloomFilter[String](100, 4)(_)
Następnie zdefiniujmy nasz zbiór danych oraz poddajmy go działaniu naszej fabryki.
val values = Seq("Ala", "ma", "kota", "a", "Tomek", "nie ma")
// values: Seq[String] = List(Ala, ma, kota, a, Tomek, nie ma)
val filters = values.map(bfBuilder)
// filters: Seq[BloomFilter[String]] = ...
Przed nami najpiękniejsza część. Złączenie wyników w jedną całość sprowadza się do zwinięcia reduceLeft naszej sekwencji za pomocą zdefiniowanego działania op (możemy też skorzystać z foldLeft podając dodatkowo element neutralny zero).
val summary = filters.reduceLeft(Monoid.op).asInstanceOf[BloomFilter[String]]
Dzięki sprowadzeniu formy naszej obliczeń do postaci monoidu, zyskujemy w naturalny sposób możliwość paralelizacji naszych obliczeń. Oznacza to, że jeśli nasz zbiór danych podzielimy i rozdystrybujemy pomiędzy kilka węzłów, przeprowadzimy na nich obliczenia, a następnie połączymy ze sobą otrzymane wyniki - za pomocą tej samej operacji, która wykonaliśmy na każdym węźle - otrzymamy ten sam rezultat, gdybyśmy cały zbiór danych przetworzyli w jednym wątku. Sprawiliśmy więc, że nasza aplikacja stała się skalowalna!
Na sam koniec upewnijmy się, że nasza struktura działa poprawnie.
scala> BloomFilter.contains(summary, "Ala")
res0: Boolean = true
scala> BloomFilter.contains(summary, "Tomek")
res1: Boolean = true
scala> BloomFilter.contains(summary, "psa")
res2: Boolean = false
Podsumowanie
Tym postem starałem się przybliżyć, w sposób przystępny dla każdego, pojęcie monoidów i ich praktycznego zastosowania w tworzeniu skalowalnych aplikacji. Jeżeli dotarłeś do tego miejsca i czujesz się przytłoczony myślą o ilości kodu, jaki musisz napisać, aby przenieść swoją aplikację w świat struktur algebraicznych, to nie musisz. Tematyka ta bowiem nie jest żadną nowością i została już dawno zgłębiona przez programistów.
- Algebird - biblioteka stworzona przez Twittera; oprócz struktur algebraicznych zawiera także implementacje wielu algorytmów aproksymacyjnych (w tym filtru Blooma)
- Scalaz, Cats - biblioteki uzupełniające braki w standardowej bibliotece Scali o struktury charakterystyczne dla programowania funkcyjnego (w tym właśnie monoidy)